Productivity
Total Factor Productivity (TFP) describes how efficiently capital and labor produce economic output. The initial value of this parameter is set to produce 2005 output given observed capital and labor in that year. webDICE assumes that TFP will continue to increase in the future, but the rate at which it increases will slow down, like a hill that is steep at the bottom and gets shallower at the top.
The default rate at which TFP growth declines is 1%. You can adjust this parameter between 0.5% and 1.5%. Higher values means growth slows down more quickly. The following figure illustrates how changing the rate at which TFP growth declines affects the evolution of productivity (the parameter is labeled $\Delta_{A}$)
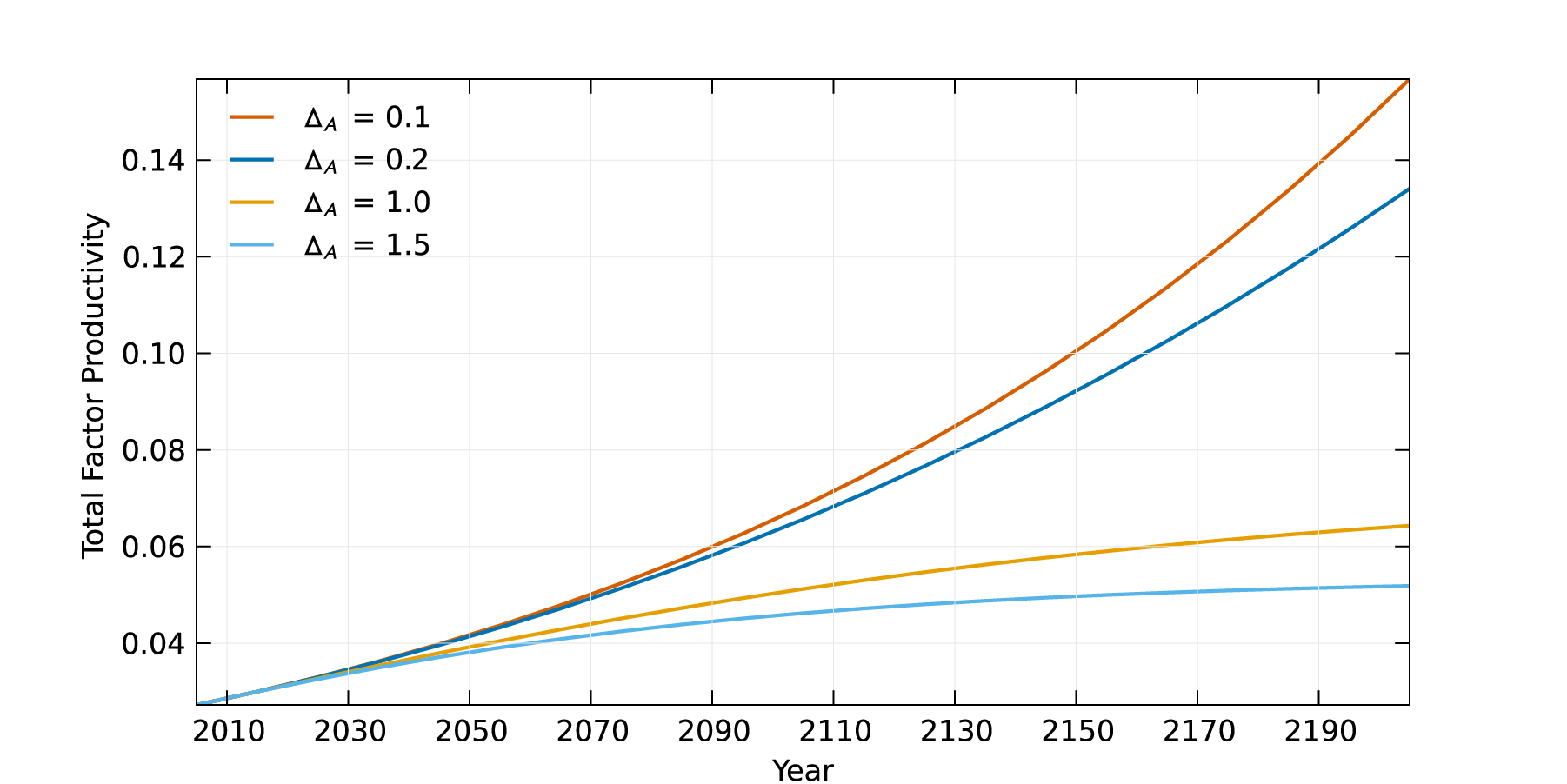
Total factor productivity (TFP), $A(t)$, describes how efficiently capital and labor produce output. The initial value, $A(0)$, is set to produce 2005 output given the observed 2005 capital and labor inputs. TPF is assumed to evolve for $t>1$, given the initial technology level according the equation: \[ A(t)=\frac{A(t-1)}{1-A_{g}(t-1)}. \] This model assumes that the rate of productivity growth, $A_{g}(t)$, will decrease in the coming decades. The following equation determines the growth rate of TFP: \[ A_{g}(t)=A_{g}(0)\times exp(-\Delta_{a}\times(t-1)). \]
The default value for $\Delta_{a}$, is ___; users can choose to adjust this parameter between ___ and ____. $\Delta_{a}$ is percentage growth rate of $A_{g}(t)$, the growth rate of TFP. To see this note that \[ \frac{d\ln A_{g}(t)}{dt}=\underset{\text{growth rate in \%}}{\underbrace{\frac{A_{g}(t+1)-A_{g}(t)}{A_{g}(t)}}=-}\Delta_{a} \] If ‘damages to TFP’ is chosen in the damages tab, a portion of damages can be applied to TFP’s levels by choosing the ‘damages to productivity growth’ damage function. See ___.